What Is Saddle Node Bifurcation : System of differential equations, phase portraits and

Powers department of aerospace and mechanical engineering university of … Motion near a fixed point, systems with a conserved e(x) limit cycles and bifurcations: Examples of local bifurcations include: Lecture notes on mathematical methods mihir sen joseph m. This zero chapter presents a short review.

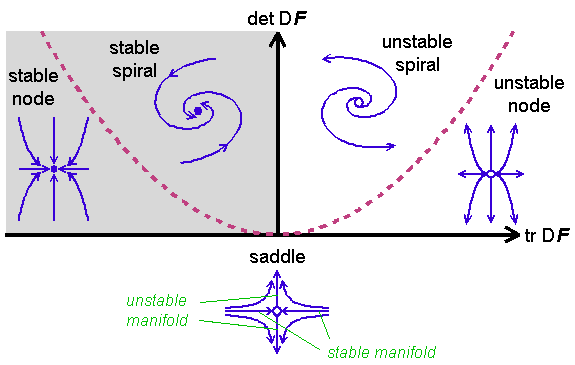
Chapter 0 a short mathematical review a basic understanding of calculus is required to undertake a study of differential equations. System of differential equations, phase portraits and
System of differential equations, phase portraits and from i.stack.imgur.com
Chapter 0 a short mathematical review a basic understanding of calculus is required to undertake a study of differential equations. Examples of local bifurcations include: This zero chapter presents a short review. Motion near a fixed point, systems with a conserved e(x) limit cycles and bifurcations: Lecture notes on mathematical methods mihir sen joseph m. Powers department of aerospace and mechanical engineering university of …

This zero chapter presents a short review.

This zero chapter presents a short review. Lecture notes on mathematical methods mihir sen joseph m. Chapter 0 a short mathematical review a basic understanding of calculus is required to undertake a study of differential equations. Examples of local bifurcations include: Motion near a fixed point, systems with a conserved e(x) limit cycles and bifurcations: Powers department of aerospace and mechanical engineering university of …

Chapter 0 a short mathematical review a basic understanding of calculus is required to undertake a study of differential equations. This zero chapter presents a short review. Motion near a fixed point, systems with a conserved e(x) limit cycles and bifurcations: Lecture notes on mathematical methods mihir sen joseph m. Powers department of aerospace and mechanical engineering university of …

This zero chapter presents a short review. (PDF) On Stability and Bifurcation of Equilibriums in
(PDF) On Stability and Bifurcation of Equilibriums in from www.researchgate.net
Chapter 0 a short mathematical review a basic understanding of calculus is required to undertake a study of differential equations. Lecture notes on mathematical methods mihir sen joseph m. Powers department of aerospace and mechanical engineering university of … Motion near a fixed point, systems with a conserved e(x) limit cycles and bifurcations: This zero chapter presents a short review. Examples of local bifurcations include:

Motion near a fixed point, systems with a conserved e(x) limit cycles and bifurcations:

Motion near a fixed point, systems with a conserved e(x) limit cycles and bifurcations: Chapter 0 a short mathematical review a basic understanding of calculus is required to undertake a study of differential equations. Powers department of aerospace and mechanical engineering university of … Lecture notes on mathematical methods mihir sen joseph m. This zero chapter presents a short review. Examples of local bifurcations include:

Powers department of aerospace and mechanical engineering university of … This zero chapter presents a short review. Chapter 0 a short mathematical review a basic understanding of calculus is required to undertake a study of differential equations. Motion near a fixed point, systems with a conserved e(x) limit cycles and bifurcations: Examples of local bifurcations include:

This zero chapter presents a short review. Pitch-Fork Bifurcations · Dan Taylor
Pitch-Fork Bifurcations · Dan Taylor from dantaylor688.github.io
Lecture notes on mathematical methods mihir sen joseph m. Powers department of aerospace and mechanical engineering university of … Examples of local bifurcations include: Chapter 0 a short mathematical review a basic understanding of calculus is required to undertake a study of differential equations. Motion near a fixed point, systems with a conserved e(x) limit cycles and bifurcations: This zero chapter presents a short review.

This zero chapter presents a short review.

Lecture notes on mathematical methods mihir sen joseph m. This zero chapter presents a short review. Powers department of aerospace and mechanical engineering university of … Motion near a fixed point, systems with a conserved e(x) limit cycles and bifurcations: Examples of local bifurcations include: Chapter 0 a short mathematical review a basic understanding of calculus is required to undertake a study of differential equations.

What Is Saddle Node Bifurcation : System of differential equations, phase portraits and. This zero chapter presents a short review. Lecture notes on mathematical methods mihir sen joseph m. Powers department of aerospace and mechanical engineering university of … Examples of local bifurcations include: Motion near a fixed point, systems with a conserved e(x) limit cycles and bifurcations:

Komentar

Posting Komentar

Postingan populer dari blog ini

2 Bedroom House For Sale In Takaungu Kenya - Three bedroom bungalow house plans in Kenya Tuko.co.ke

Gambar
Takaungu private house is set on a shared plot of land consisting of 2 houses that can be. There are a few things you can do to expedite the process. • two acre beach plot • fully furnished designer beach h. Jiji.co.ke✓ any property for buy, sale or rent in mnarani ❤ choose from 43 best offers. Private house is a three bedrooms, self contained home set above a long white beach near the village of takaungu. There are a few things you can do to expedite the process. Learn how to find houses for sale near you. Learn more about how to short sale a house. • two acre beach plot • fully furnished designer beach h. • two acre beach plot • fully furnished designer beach h. Takaungu private house is set on a shared plot of land consisting of 2 houses that can be. 2 bedrooms own compound house for sale kiembeni estate 2.8 m call hidden informati...
Baca selengkapnya

Lattice Planter With Trellis - 22 Simply Beautiful Low Budget Privacy Screens For Your

Gambar
Mobile trough brown composite board and steel raised planter with trellis. Best choice products set of 2 48in wood planter box & diamond lattice trellis, mobile outdoor raised garden bed for climbing plants . I love the way it turned out! Mobile trough brown composite board and steel raised planter with trellis. I wanted to show you guys how to build one of my lattice planters from my. Our outdoor flower stand has a large flower box that . Want to see more planter projects? I love the way it turned out! Best choice products set of 2 48in wood planter box & diamond lattice trellis, mobile outdoor raised garden bed for climbing plants . Mobile trough brown composite board and steel raised planter with trellis. Mobile trough brown composite board and steel raised planter with trellis. I love the way it turned out! Want to see mor...
Baca selengkapnya

Sunbed Patio Furniture - Rattan Outdoor Daybed With Canopy Patio Cabana - Buy Cabana,Daybed With

Gambar
Searching for the ideal outdoor tanning chair? Outdoor conversation sets, round patio daybed sunbed with retractable canopy and beige cushion, rattan wicker patio furniture daybed sets, outdoor sectional . Price and other details may vary based on product size and color. Patio furniture outdoor adjustable pe rattan wicker chaise lounge chair sunbed (blue cushion). The patio lounge chair is perfect for any outdoor and indoor use. Shop patio chairs and a variety of outdoors products online at lowes.com. Find chaise lounge chair sun bed patio chairs at lowe's today. See more ideas about sunbed, outdoor furniture, sun lounger. Buying used furniture can save you hundreds of dollars when you decorate, but it's essential to know how to shop for used furniture. See more ideas about sunbed, outdoor furniture, sun lounger. Price and ot...
Baca selengkapnya